Gaussian Pulse

The Gaussian pulse of width (second central moment) 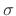$\sigma$ centered on time 0 may be defined by

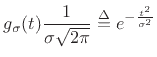$$g_\sigma(t) \frac{1}{\sigma\sqrt{2\pi}}\isdef e^{-\frac{t^2}{\sigma^2}}$$ (B.29)

where the normalization scale factor is chosen to give unit area under the pulse. Its Fourier transform is derived in Appendix D to be

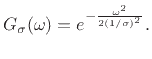$$G_\sigma(\omega) = e^{-\frac{\omega^2}{2(1/\sigma)^2}}.$$ (B.30)