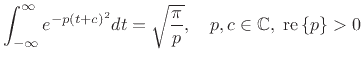 |
(D.12) |
Theorem:
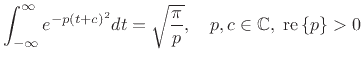 |
(D.12) |
Proof:
When ![]() , we have the previously proved case. For arbitrary
, we have the previously proved case. For arbitrary
![]() and real number
and real number
![]() , let
, let
![]() denote the closed rectangular contour
denote the closed rectangular contour
![]() , depicted in Fig.D.1.
, depicted in Fig.D.1.
Clearly,
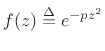 is analytic inside the region bounded
by
is analytic inside the region bounded
by
![]() . By Cauchy's theorem [42],
the line integral of
. By Cauchy's theorem [42],
the line integral of ![]() along
along
![]() is zero, i.e.,
is zero, i.e.,
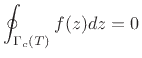 |
(D.13) |
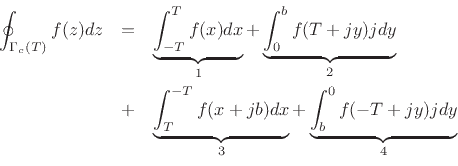
where ![]() and
and ![]() are real variables. In the limit as
are real variables. In the limit as
![]() ,
the first piece approaches
,
the first piece approaches
![]() , as previously proved.
Pieces
, as previously proved.
Pieces ![]() and
and ![]() contribute zero in the limit, since
contribute zero in the limit, since
![]() as
as
![]() . Since the total contour integral is
zero by Cauchy's theorem, we conclude that piece 3 is the negative of
piece 1, i.e., in the limit as
. Since the total contour integral is
zero by Cauchy's theorem, we conclude that piece 3 is the negative of
piece 1, i.e., in the limit as
![]() ,
,
 |
(D.14) |
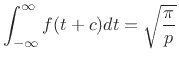 |
(D.15) |