Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Gaussian Characteristic Function
Since the Gaussian PDF is
 |
(D.50) |
and since the Fourier transform of 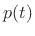 is
is
 |
(D.51) |
It follows that the Gaussian characteristic function is
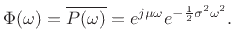 |
(D.52) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]

