Fourier Transform (FT) and Inverse

The Fourier transform of a signal 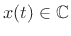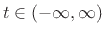$x(t)\in\mathbb{C}$ , $t\in(-\infty,\infty)$ , is defined as

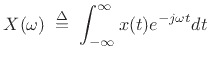$$X(\omega) \isdefs \int_{-\infty}^\infty x(t) e^{-j\omega t} dt \protect$$ (3.4)

and its inverse is given by

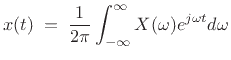$$x(t) \eqsp \frac{1}{2\pi}\int_{-\infty}^\infty X(\omega) e^{j\omega t} d\omega \protect$$ (3.5)

Thus, the Fourier transform is defined for continuous time and continuous frequency, both unbounded. As a result, mathematical questions such as existence and invertibility are most difficult for this case. In fact, such questions fueled decades of confusion in the history of harmonic analysis (see Appendix G).