Downsampling (Decimation) Operator

Figure: Downsampling by $N$ .

Figure 11.3 shows the symbol for downsampling by the factor $N$ . The downsampler selects every $N$ th sample and discards the rest:

$$\begin{eqnarray*} y(n) &=& \hbox{\sc Downsample}_{N,n}(x)\\ &\isdef & x(Nn), \quad n\in\mathbb{Z} \end{eqnarray*}$$

In the frequency domain, we have

$$\begin{eqnarray*} Y(z) &=& \hbox{\sc Alias}_{N,z}(X)\\ &\isdef & \frac{1}{N} \sum_{m=0}^{N-1} X\left(z^\frac{1}{N}e^{-jm\frac{2\pi}{N}} \right), \quad z\in\mathbb{C}. \end{eqnarray*}$$

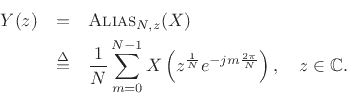
Thus, the frequency axis is expanded by the factor $N$ , wrapping $N$ times around the unit circle, adding to itself $N$ times. For $N=2$ , two partial spectra are summed, as indicated in Fig.11.4.

Figure: Illustration of $\hbox {\sc Alias}_2$ in the frequency domain.

Using the common twiddle factor notation

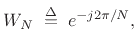$$W_N \isdefs e^{-j2\pi/N},$$ (12.1)

the aliasing expression can be written as

$$Y(z) \eqsp \frac{1}{N} \sum_{m=0}^{N-1} X(W_N^m z^{1/N}).$$