The downsampling operator
![]() selects every
selects every ![]() sample of a signal:
sample of a signal:
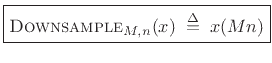 |
(3.32) |
The aliasing theorem states that downsampling in time corresponds to aliasing in the frequency domain:
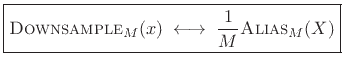 |
(3.33) |
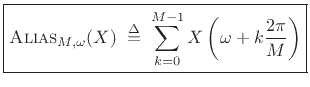 |
(3.34) |
In z transform notation, the
![]() operator can be expressed as
[287]
operator can be expressed as
[287]
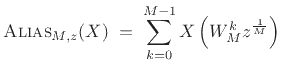 |
(3.35) |
![$\displaystyle \hbox{\sc Alias}_{M,\omega}(X) \eqsp \sum_{k=0}^{M-1} X\left[e^{j\left(\frac{\omega}{M} + k\frac{2\pi}{M}\right)}\right], \quad -\pi\leq \omega < \pi.$](img217.png) |
(3.36) |
The aliasing theorem makes it clear that, in order to downsample by
factor ![]() without aliasing, we must first lowpass-filter the spectrum
to
without aliasing, we must first lowpass-filter the spectrum
to
![]() . This filtering (when ideal) zeroes out the
spectral regions which alias upon downsampling.
. This filtering (when ideal) zeroes out the
spectral regions which alias upon downsampling.
Note that any rational sampling-rate conversion factor
![]() may be implemented as an upsampling by the factor
may be implemented as an upsampling by the factor ![]() followed by
downsampling by the factor
followed by
downsampling by the factor ![]() [50,287].
Conceptually, a stretch-by-
[50,287].
Conceptually, a stretch-by-![]() is followed by a lowpass filter cutting
off at
is followed by a lowpass filter cutting
off at
![]() , followed by
downsample-by-
, followed by
downsample-by-![]() , i.e.,
, i.e.,
| (3.37) |