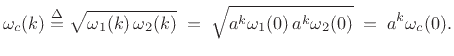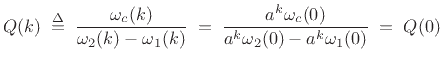Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The discrete wavelet transform is a discrete-time,
discrete-frequency counterpart of the continuous wavelet transform of
the previous section:
where 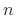 and
and 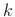 range over the integers, and
range over the integers, and  is the mother
wavelet, interpreted here as a (continuous) filter impulse response.
is the mother
wavelet, interpreted here as a (continuous) filter impulse response.
The inverse transform is, as always, the signal expansion in terms of
the orthonormal basis set:
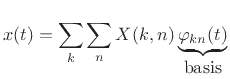 |
(12.120) |
We can show that discrete wavelet transforms are constant-Q by
defining the center frequency of the 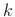 th basis signal as the
geometric mean of its bandlimits
th basis signal as the
geometric mean of its bandlimits 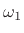 and
and 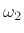 , i.e.,
, i.e.,
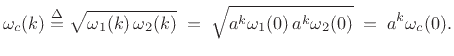 |
(12.121) |
Then
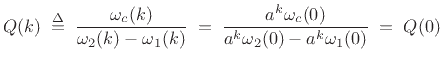 |
(12.122) |
which does not depend on 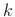 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
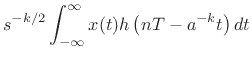

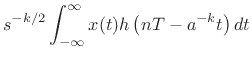

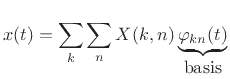
![]() th basis signal as the
geometric mean of its bandlimits
th basis signal as the
geometric mean of its bandlimits ![]() and
and ![]() , i.e.,
, i.e.,