Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The DTFT at frequency 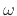 is given by
is given by
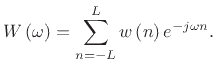 |
(4.69) |
By zero-phase symmetry,
So
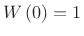 can be expressed as
can be expressed as
 |
(4.70) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() is given by
is given by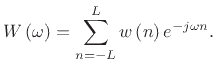
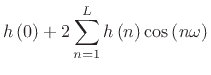
![$\displaystyle \left[\begin{array}{cccc}
1 & 2\cos \left(\omega \right) & \cdots & 2\cos \left(L\omega \right)\end{array}\right]\left[\begin{array}{c}
h\left(0\right)\\
h\left(1\right)\\
\vdots \\
h\left(L\right)\end{array}\right]$](img598.png)
