Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
If
![$h(t)\in[-1,1-2^{-n_c}]$](img89.png) is approximated by hq(t) which is
represented in two's complement fixed-point
arithmetic, then
is approximated by hq(t) which is
represented in two's complement fixed-point
arithmetic, then
where 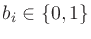 is the ith bit,
and the worst-case rounding error is
is the ith bit,
and the worst-case rounding error is
Letting
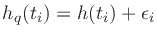 , where
, where
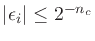 ,
the interpolated look-up becomes
,
the interpolated look-up becomes
Thus the error in the interpolated
lookup between quantized filter coefficients is bounded by
which, in the case of
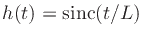 , can be written
, can be written
If L=2nc/2, then
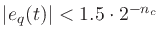 .
.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download resample.pdf
[How to cite and copy this work] [Comment on this page via email]
![]() is approximated by hq(t) which is
represented in two's complement fixed-point
arithmetic, then
is approximated by hq(t) which is
represented in two's complement fixed-point
arithmetic, then
