Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The quantized interpolation factor and its complement are representable as
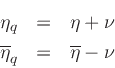
where, since
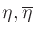 are unsigned,
are unsigned,
 .
The interpolated coefficient look-up then gives
.
The interpolated coefficient look-up then gives
![\begin{eqnarray*}
\hat{h}_{qq}(t) &=& (\overline{\eta }-\nu)[h(t_0)+\epsilon_0] + (\eta+\nu)[h(t_1)+\epsilon_1] \\
&=& \hat{h}(t) + \overline{\eta }\epsilon_0 + \eta\epsilon_1 + \nu[h(t_1)-h(t_0)],
\end{eqnarray*}](img109.png)
where second-order errors 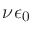 and
and 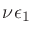 are dropped.
Since
are dropped.
Since
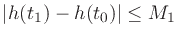 , we obtain the error bound
, we obtain the error bound
 |
(14) |
The three terms in Eq.(14) are caused by coefficient quantization,
interpolation quantization, and linear-approximation error, respectively.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download resample.pdf
[How to cite and copy this work] [Comment on this page via email]
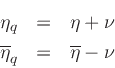
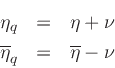
![]() are unsigned,
are unsigned,
![]() .
The interpolated coefficient look-up then gives
.
The interpolated coefficient look-up then gives
![\begin{eqnarray*}
\hat{h}_{qq}(t) &=& (\overline{\eta }-\nu)[h(t_0)+\epsilon_0] + (\eta+\nu)[h(t_1)+\epsilon_1] \\
&=& \hat{h}(t) + \overline{\eta }\epsilon_0 + \eta\epsilon_1 + \nu[h(t_1)-h(t_0)],
\end{eqnarray*}](img109.png)
![]() and
and ![]() are dropped.
Since
are dropped.
Since
![]() , we obtain the error bound
, we obtain the error bound