Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Let h(t) denote the lowpass filter impulse response, and assume it is
twice continuously differentiable for all t. By Taylor's theorem
[#!Goldstein!#, p. 119], we have
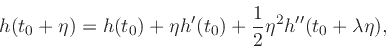 |
(6) |
for some
![$\lambda \in[0,1]$](img60.png) , where
, where
 denotes the time derivative of
h(t) evaluated at t=t0, and
denotes the time derivative of
h(t) evaluated at t=t0, and
 is the second derivative at
t0.
is the second derivative at
t0.
The linear interpolation error is
 |
(7) |
where  ,
,
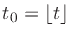 ,
, 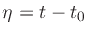 , and
, and
 is the interpolated value given by
is the interpolated value given by
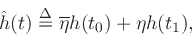 |
(8) |
where
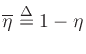 and
and
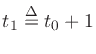 . Thus t0 and t1 are
successive time instants for which samples of h(t) are available,
and
. Thus t0 and t1 are
successive time instants for which samples of h(t) are available,
and 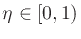 is the linear interpolation factor.
is the linear interpolation factor.
By definition,
e(t0)=e(t1)=0. That is, the interpolation error is
zero at the known samples. Let te denote any point at which
|e(t)| reaches a maximum over the interval (t0,t1). Then we
have
Without loss of generality, assume
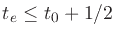 . (Otherwise,
replace t0 with t1 in the following.) Since both h(t) and
. (Otherwise,
replace t0 with t1 in the following.) Since both h(t) and
 are twice differentiable for all
are twice differentiable for all 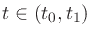 , then so is
e(t), and therefore e'(te)=0. Expressing e(t0)=0 as a Taylor
expansion of e(t) about t=te, we obtain
, then so is
e(t), and therefore e'(te)=0. Expressing e(t0)=0 as a Taylor
expansion of e(t) about t=te, we obtain
for some
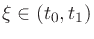 . Solving for e(te) gives
. Solving for e(te) gives
Defining
where the maximum is taken over 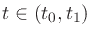 , and noting that
, and noting that
 , we obtain the upper bound2
, we obtain the upper bound2
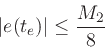 |
(9) |
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download resample.pdf
[How to cite and copy this work] [Comment on this page via email]
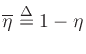 and
and
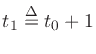 . Thus t0 and t1 are
successive time instants for which samples of h(t) are available,
and
. Thus t0 and t1 are
successive time instants for which samples of h(t) are available,
and