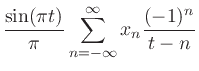Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
It is interesting to note that all periodic sampled signals can
be sinc-interpolated exactly using the following formula
[#!Schanze!#]:
where the sampling rate is normalized to be T=1, and the period is
N = L + M samples.
The first step in the derivation is the exact general formula
| x(t) |
= |
![$\displaystyle \sum_{n = -\infty}^{\infty} x_n {\sin[\pi (t-n)] \over \pi(t-n)}$](img118.png) |
(15) |
| |
= |
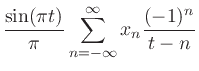 |
(16) |
which follows immediately from the identity
![$\sin[\pi(t-n)] =
(-1)^n\sin(\pi t)$](img120.png) . This form can be used to develop a table-based sinc
interpolation algorithm in which the function 1/t is sampled, windowed,
and stored in a table over a small range of t. (Reverting to the
weighted sinc table is advisable near an argument of zero where there is a
pole-zero cancellation in the definition of
. This form can be used to develop a table-based sinc
interpolation algorithm in which the function 1/t is sampled, windowed,
and stored in a table over a small range of t. (Reverting to the
weighted sinc table is advisable near an argument of zero where there is a
pole-zero cancellation in the definition of  , i.e., when
, i.e., when
 .) Note that when t crosses 2, the 1/t table can be
implemented as
(1/2)(1/(t/2)). In other words, the table between t=2
and t=4 can be computed from the table between t=1 and t=2 using a
simple one-bit right-shift on the table address and the table output. If
this trick is used, the table window must be applied separately, but there
ways to synthesize simple windows (e.g., the Hanning or Hamming windows
which consist of a single sinusoidal component) using waveform synthesis
techniques, avoiding a separate table for the interpolated window function.
.) Note that when t crosses 2, the 1/t table can be
implemented as
(1/2)(1/(t/2)). In other words, the table between t=2
and t=4 can be computed from the table between t=1 and t=2 using a
simple one-bit right-shift on the table address and the table output. If
this trick is used, the table window must be applied separately, but there
ways to synthesize simple windows (e.g., the Hanning or Hamming windows
which consist of a single sinusoidal component) using waveform synthesis
techniques, avoiding a separate table for the interpolated window function.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download resample.pdf
[How to cite and copy this work] [Comment on this page via email]
![\begin{displaymath}
x(t) = {\sin(\pi t) \over 2N} \sum_{n = -L}^{M-1}
x_n (-1)^n \left[ (-1)^{N+1} \tan\left(\pi {t-n \over 2N} \right)
+ \cot\left(\pi {t-n \over 2N} \right) \right],
\quad N=L+M
\end{displaymath}](img117.png)
![\begin{displaymath}
x(t) = {\sin(\pi t) \over 2N} \sum_{n = -L}^{M-1}
x_n (-1)^n \left[ (-1)^{N+1} \tan\left(\pi {t-n \over 2N} \right)
+ \cot\left(\pi {t-n \over 2N} \right) \right],
\quad N=L+M
\end{displaymath}](img117.png)
![$\displaystyle \sum_{n = -\infty}^{\infty} x_n {\sin[\pi (t-n)] \over \pi(t-n)}$](img118.png)