Sinusoid Magnitude Spectra

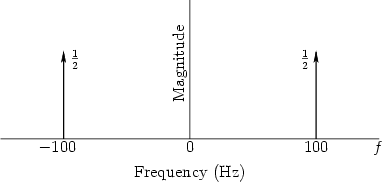
A sinusoid's frequency content may be graphed in the frequency domain as shown in Fig. 1.

Figure 1: Spectral magnitude representation of a unit-amplitude sinusoid at frequency $100$ Hz such as $\cos(200\pi t)$ or $\sin(200\pi t$). (Phase is not shown.)

An example of a particular sinusoid graphed in Fig. 1 is given by

$$x(t) = \cos(\omega_x t) = \frac{1}{2}e^{j\omega_x t} + \frac{1}{2}e^{-j\omega_x t}$$

where

$$\omega_x = 2\pi 100.$$

That is, this sinusoid has amplitude 1, frequency 100 Hz, and phase zero (or $\pi/2$, if $\sin(\omega_x t)$ is defined as the zero-phase case).

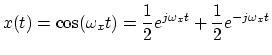
Figure 1 can be viewed as a graph of the magnitude spectrum of $x(t)$, or its spectral magnitude representation [4]. Note that the spectrum consists of two components with amplitude $1/2$, one at frequency $100$ Hz and the other at frequency $-100$ Hz.

Phase is not shown in Fig. 1 at all. The phase of the components could be written simply as labels next to the magnitude arrows, or the magnitude arrows can be rotated ``into or out of the page'' by the appropriate phase angle as illustrated in [7, Fig. 4.8 on p. 43].