Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
FM Spectra
Using the expansion in Eq. (7), it is now easy to determine
the spectrum of sinusoidal FM. Eliminating scaling and
phase offsets for simplicity
in Eq. (5) yields
![$\displaystyle x(t) = \cos[\omega_c t + \beta\sin(\omega_m t)]. \protect$](img80.png) |
(8) |
where we have changed the modulator amplitude 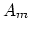 to the more
traditional symbol
to the more
traditional symbol 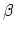 , called the FM index in FM sound
synthesis contexts. Using phasor analysis,
, called the FM index in FM sound
synthesis contexts. Using phasor analysis,
where we used the fact that
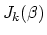 is real when
is real when 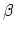 is real.
We can now see clearly that the sinusoidal FM spectrum consists of an
infinite number of side-bands about the carrier frequency
is real.
We can now see clearly that the sinusoidal FM spectrum consists of an
infinite number of side-bands about the carrier frequency 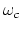 (when
(when
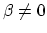 ). The side bands occur at multiples of the
modulating frequency
). The side bands occur at multiples of the
modulating frequency 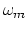 away from the carrier frequency
away from the carrier frequency
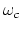
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download rbeats.pdf
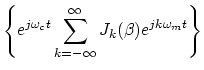
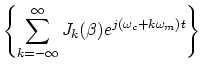
![$\displaystyle \sum_{k=-\infty}^\infty J_k(\beta) \cos[(\omega_c+k\omega_m) t]$](img88.png)