Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Prime Factor Algorithm
(PFA)
By the prime factorization theorem, every integer 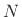 can be uniquely
factored into a product of prime numbers
can be uniquely
factored into a product of prime numbers  raised to an
integer power
raised to an
integer power 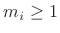 :
:
As discussed above, a mixed-radix Cooley Tukey FFT can be used to
implement a length 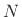 DFT using DFTs of length
DFT using DFTs of length  . However, for
factors of
. However, for
factors of 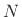 that are mutually prime (such as
that are mutually prime (such as 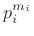 and
and
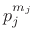 for
for 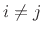 ), a more efficient prime factor
algorithm (PFA), also called the Good-Thomas FFT algorithm,
can be used [27,83,36,45,10,86].A.4
The Chinese Remainder
Theorem
is used to re-index either the input or output samples for the PFA.A.5Since the PFA is only applicable to mutually prime factors of
), a more efficient prime factor
algorithm (PFA), also called the Good-Thomas FFT algorithm,
can be used [27,83,36,45,10,86].A.4
The Chinese Remainder
Theorem
is used to re-index either the input or output samples for the PFA.A.5Since the PFA is only applicable to mutually prime factors of 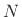 , it
is ideally combined with a mixed-radix Cooley-Tukey FFT, which works
for any integer factors.
, it
is ideally combined with a mixed-radix Cooley-Tukey FFT, which works
for any integer factors.
It is interesting to note that the PFA actually predates the
Cooley-Tukey FFT paper of 1965 [17], with Good's
1958 work on the PFA being cited in that paper [86].
The PFA and Winograd transform [45] are
closely related, with the PFA being somewhat faster [9].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() can be uniquely
factored into a product of prime numbers
can be uniquely
factored into a product of prime numbers ![]() raised to an
integer power
raised to an
integer power ![]() :
: