Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Definition: The phase response of a filter is defined as
the phase of its frequency response:
From the convolution theorem, we can see that the phase response
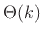 is the phase-shift added by the filter to an input sinusoidal
component at frequency
is the phase-shift added by the filter to an input sinusoidal
component at frequency 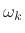 , since
, since
The topics touched upon in this section are developed more fully in
the next book [71] in the music signal processing series
mentioned in the preface.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]