Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Factoring a Polynomial
Remember ``factoring polynomials''? Consider the second-order polynomial
It is second-order because the highest power of 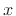 is
is 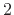 (only
non-negative integer powers of
(only
non-negative integer powers of 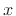 are allowed in this context). The
polynomial is also
monic
because its leading coefficient, the
coefficient of
are allowed in this context). The
polynomial is also
monic
because its leading coefficient, the
coefficient of 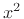 , is
, is 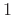 . By the fundamental theorem of algebra
(discussed further in §2.4), there are exactly two
roots
(or
zeros) of any
second order polynomial. These roots may be real or complex (to be defined).
For now, let's assume they are both real and denote them by
. By the fundamental theorem of algebra
(discussed further in §2.4), there are exactly two
roots
(or
zeros) of any
second order polynomial. These roots may be real or complex (to be defined).
For now, let's assume they are both real and denote them by
 and
and 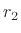 . Then we have
. Then we have
 and
and 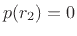 , and we can write
, and we can write
This is the factored form of the monic polynomial 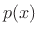 .
(For a non-monic polynomial, we may simply divide all coefficients
by the first to make it monic, and this doesn't affect the zeros.)
Multiplying out the symbolic factored form gives
.
(For a non-monic polynomial, we may simply divide all coefficients
by the first to make it monic, and this doesn't affect the zeros.)
Multiplying out the symbolic factored form gives
Comparing with the original polynomial, we find we must have
This is a system of two equations in two unknowns. Unfortunately, it is a
nonlinear system of two equations in two
unknowns.2.1 Nevertheless, because it is so small,
the equations are easily solved. In beginning algebra, we did them by
hand. However, nowadays we can use a software tool such as Matlab or
Octave to solve very large systems of linear equations.
The factored form of this simple example is
Note that polynomial factorization rewrites a monic  th-order
polynomial as the product of
th-order
polynomial as the product of  first-order monic polynomials,
each of which contributes one zero (root) to the product. This
factoring business is often used when working with digital
filters [71].
first-order monic polynomials,
each of which contributes one zero (root) to the product. This
factoring business is often used when working with digital
filters [71].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]