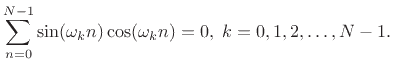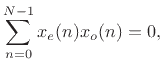Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Some of the Fourier theorems can be succinctly expressed in terms of even
and odd symmetries.
Definition: A function 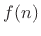 is said to be even if
is said to be even if
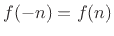 .
.
An even function is also symmetric, but the
term symmetric applies also to functions symmetric about a point other
than 0
.
Definition: A function 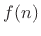 is said to be odd if
is said to be odd if
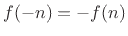 .
.
An odd function is also called antisymmetric.
Note that every finite odd function 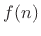 must satisfy
must satisfy
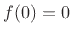 .7.12 Moreover, for any
.7.12 Moreover, for any
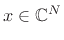 with
with
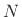 even, we also have
even, we also have 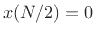 since
since
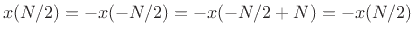 ; that is,
; that is, 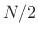 and
and 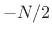 index
the same point when
index
the same point when 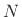 is even (since all indexing in
is even (since all indexing in
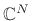 is modulo
is modulo 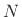 ).
).
Theorem: Every function 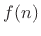 can be
uniquely
decomposed into a sum of its even part
can be
uniquely
decomposed into a sum of its even part
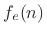 and odd part
and odd part 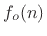 , where
, where
Proof: In the above definitions, 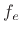 is even and
is even and 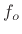 is odd by construction.
Summing, we have
is odd by construction.
Summing, we have
To show uniqueness, let
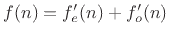 denote some other
even-odd decomposition. Then
denote some other
even-odd decomposition. Then
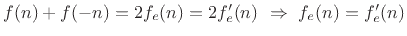 , and
, and
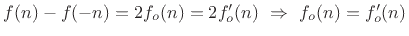 .
.
Theorem: The product of even functions is even, the product of odd functions
is even, and the product of an even times an odd function is odd.
Proof: Readily shown.
Since even times even is even, odd times odd is even, and even times odd is
odd, we can think of even as 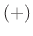 and odd as
and odd as 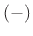 :
:
Example:
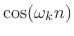 ,
,
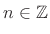 , is an
even signal since
, is an
even signal since
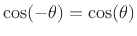 .
.
Example:
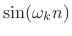 is an odd signal since
is an odd signal since
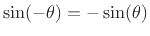 .
.
Example:
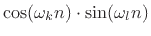 is an odd signal (even times odd).
is an odd signal (even times odd).
Example:
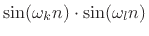 is an even signal (odd times odd).
is an even signal (odd times odd).
Theorem: The sum of all the samples of an odd signal 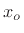 in
in
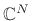 is zero.
is zero.
Proof: This is readily shown by writing the sum as
![$ x_o(0) + [x_o(1) + x_o(-1)]
+ \cdots + x(N/2)$](img1301.png) , where the last term only occurs when
, where the last term only occurs when 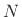 is even. Each
term so written is zero for an odd signal
is even. Each
term so written is zero for an odd signal 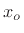 .
.
Example: For all DFT sinusoidal frequencies
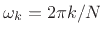 ,
,
More generally,
for any even signal 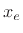 and odd signal
and odd signal 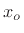 in
in
 . In
terms of inner products (§5.9), we may say that the even part
of every real signal is orthogonal to its odd part:
. In
terms of inner products (§5.9), we may say that the even part
of every real signal is orthogonal to its odd part:
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() is said to be even if
is said to be even if
![]() .
.
![]() is said to be odd if
is said to be odd if
![]() .
.
![]() must satisfy
must satisfy
![]() .7.12 Moreover, for any
.7.12 Moreover, for any
![]() with
with
![]() even, we also have
even, we also have ![]() since
since
![]() ; that is,
; that is, ![]() and
and ![]() index
the same point when
index
the same point when ![]() is even (since all indexing in
is even (since all indexing in
![]() is modulo
is modulo ![]() ).
).
![]() can be
uniquely
decomposed into a sum of its even part
can be
uniquely
decomposed into a sum of its even part
![]() and odd part
and odd part ![]() , where
, where
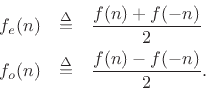
![]() is even and
is even and ![]() is odd by construction.
Summing, we have
is odd by construction.
Summing, we have
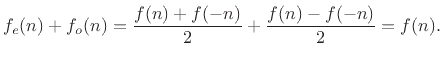
![]() and odd as
and odd as ![]() :
:
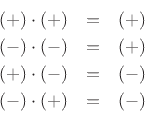
![]() ,
,
![]() , is an
even signal since
, is an
even signal since
![]() .
.
![]() is an odd signal since
is an odd signal since
![]() .
.
![]() is an odd signal (even times odd).
is an odd signal (even times odd).
![]() is an even signal (odd times odd).
is an even signal (odd times odd).
![]() in
in
![]() is zero.
is zero.
![]() , where the last term only occurs when
, where the last term only occurs when ![]() is even. Each
term so written is zero for an odd signal
is even. Each
term so written is zero for an odd signal ![]() .
.
![]() ,
,