Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Downsampling Operator
Downsampling by 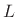 (also called decimation by
(also called decimation by 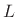 ) is defined
for
) is defined
for
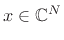 as taking every
as taking every 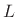 th sample, starting with sample zero:
th sample, starting with sample zero:
The
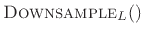 operator maps a length
operator maps a length 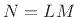 signal down to a length
signal down to a length 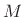 signal. It is the inverse of the
signal. It is the inverse of the
 operator (but not vice
versa), i.e.,
operator (but not vice
versa), i.e.,
The stretch and downsampling operations do not commute because they are
linear time-varying operators. They can be modeled using
time-varying switches controlled by the sample index  .
.
Figure 7.10:
Illustration of
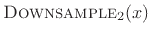 .
.
![\includegraphics[width=4in]{eps/downsamplex}](img1260.png) |
The following example of
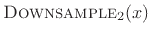 is illustrated in Fig.7.10:
is illustrated in Fig.7.10:
Note that the term ``downsampling'' may also refer to the more
elaborate process of sampling-rate conversion to a lower
sampling rate, in which a signal's sampling rate is lowered by resampling
using bandlimited interpolation. To distinguish these cases, we can call
this bandlimited downsampling, because a lowpass-filter is
needed, in general, prior to downsampling so that aliasing is
avoided. This topic is address in Appendix D. Early
sampling-rate converters were in fact implemented using the
 operation, followed by an appropriate lowpass filter,
followed by
operation, followed by an appropriate lowpass filter,
followed by
 , in order to implement a sampling-rate
conversion by the factor
, in order to implement a sampling-rate
conversion by the factor 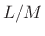 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() (also called decimation by
(also called decimation by ![]() ) is defined
for
) is defined
for
![]() as taking every
as taking every ![]() th sample, starting with sample zero:
th sample, starting with sample zero:
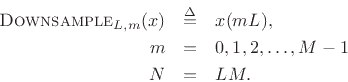
![]() operator maps a length
operator maps a length ![]() signal down to a length
signal down to a length ![]() signal. It is the inverse of the
signal. It is the inverse of the
![]() operator (but not vice
versa), i.e.,
operator (but not vice
versa), i.e.,
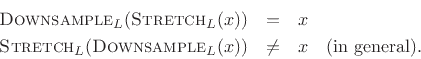
![]() .
.
![]() is illustrated in Fig.7.10:
is illustrated in Fig.7.10:
![]() operation, followed by an appropriate lowpass filter,
followed by
operation, followed by an appropriate lowpass filter,
followed by
![]() , in order to implement a sampling-rate
conversion by the factor
, in order to implement a sampling-rate
conversion by the factor ![]() .
.