Because ![]() is an eigenfunction under differentiation
(i.e., the exponential function is its own derivative), it is often
profitable to replace it with a generalized exponential function, with
maximum degrees of freedom in its parametrization, to see if
parameters can be found to fulfill the constraints imposed by differential
equations.
is an eigenfunction under differentiation
(i.e., the exponential function is its own derivative), it is often
profitable to replace it with a generalized exponential function, with
maximum degrees of freedom in its parametrization, to see if
parameters can be found to fulfill the constraints imposed by differential
equations.
In the case of the one-dimensional ideal wave equation (Eq. (G.1)), with no boundary conditions, an appropriate choice of eigensolution is
| (G.12) |
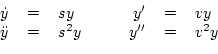
| (G.13) | |||