Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
If we relax the constraint that
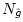 be odd, then the simplest case
becomes the one-zero digital filter:
be odd, then the simplest case
becomes the one-zero digital filter:
When
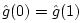 , the filter is linear phase, and its
phase delay and group delay are equal to
, the filter is linear phase, and its
phase delay and group delay are equal to 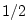 sample [340].
In practice, the half-sample delay must be compensated elsewhere in the
filtered delay loop, such as in the delay-line interpolation filter
[194].
Normalizing the dc gain to unity removes the last degree of freedom
so that
sample [340].
In practice, the half-sample delay must be compensated elsewhere in the
filtered delay loop, such as in the delay-line interpolation filter
[194].
Normalizing the dc gain to unity removes the last degree of freedom
so that
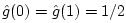 , and
, and
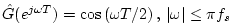 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() be odd, then the simplest case
becomes the one-zero digital filter:
be odd, then the simplest case
becomes the one-zero digital filter: