Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
An arbitrary interconnection of 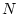 impedances and admittances, with input
and output force and/or velocities defined, results in a one-port with
admittance expressible as
impedances and admittances, with input
and output force and/or velocities defined, results in a one-port with
admittance expressible as
In any mechanical situation we have 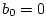 , in principle, since at
sufficiently high frequencies, every mechanical system must ``look like
a mass.''J.2 However,
for purposes of
approximation to a real physical system, it may well be best to
allow
, in principle, since at
sufficiently high frequencies, every mechanical system must ``look like
a mass.''J.2 However,
for purposes of
approximation to a real physical system, it may well be best to
allow 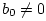 and consider the above expression to be a
rational approximation to the true admittance function.
and consider the above expression to be a
rational approximation to the true admittance function.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() impedances and admittances, with input
and output force and/or velocities defined, results in a one-port with
admittance expressible as
impedances and admittances, with input
and output force and/or velocities defined, results in a one-port with
admittance expressible as