Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Let
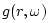 denote the decay factor associated with
propagation of a plane wave over distance
denote the decay factor associated with
propagation of a plane wave over distance 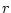 at frequency
at frequency
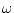 rad/sec. For an ideal plane wave, there is no ``spreading
loss'' (attenuation by
rad/sec. For an ideal plane wave, there is no ``spreading
loss'' (attenuation by 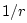 ). Under uniform conditions, the
amount of attenuation (in dB) is proportional to the distance
traveled; in other words, the attenuation factors for two successive
segments of a propagation path are multiplicative:
). Under uniform conditions, the
amount of attenuation (in dB) is proportional to the distance
traveled; in other words, the attenuation factors for two successive
segments of a propagation path are multiplicative:
This property implies that 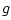 is an exponential function of
distance
is an exponential function of
distance 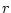 .2.3
.2.3
Frequency-independent air
absorption is easily modeled in an acoustic simulation by making
the substitution
in the transfer function of the simulating delay line, where 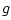 denotes the attenuation associated with propagation during one
sampling period (
denotes the attenuation associated with propagation during one
sampling period (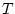 seconds). Thus, to simulate absorption
corresponding to an
seconds). Thus, to simulate absorption
corresponding to an 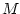 -sample delay, the difference equation
Eq. (1.1) on page
-sample delay, the difference equation
Eq. (1.1) on page ![[*]](../icons/crossref.png) becomes
as depicted in Fig. 1.8.
becomes
as depicted in Fig. 1.8.
More generally, frequency-dependent air
absorption can be modeled using the substitution
where 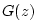 denotes the filtering per sample in the
propagation medium. Since air absorption cannot amplify a wave at any
frequency, we have
denotes the filtering per sample in the
propagation medium. Since air absorption cannot amplify a wave at any
frequency, we have
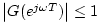 . A lossy delay line for
plane-wave simulation is thus described by
in the frequency domain, and
in the time domain, where `
. A lossy delay line for
plane-wave simulation is thus described by
in the frequency domain, and
in the time domain, where `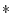 ' denotes convolution, and
' denotes convolution, and 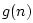 is
the impulse response of the per-sample loss filter
is
the impulse response of the per-sample loss filter 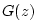 .
.
For spherical waves, the loss due to spherical spreading is of the form
where 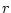 is the distance from
is the distance from 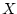 to
to 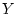 . We see that the spherical
spreading loss factor is ``hyperbolic'' in the propagation distance
. We see that the spherical
spreading loss factor is ``hyperbolic'' in the propagation distance
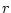 , while air absorption is exponential in
, while air absorption is exponential in 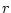 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite and copy this work]
![]() denote the decay factor associated with
propagation of a plane wave over distance
denote the decay factor associated with
propagation of a plane wave over distance ![]() at frequency
at frequency
![]() rad/sec. For an ideal plane wave, there is no ``spreading
loss'' (attenuation by
rad/sec. For an ideal plane wave, there is no ``spreading
loss'' (attenuation by ![]() ). Under uniform conditions, the
amount of attenuation (in dB) is proportional to the distance
traveled; in other words, the attenuation factors for two successive
segments of a propagation path are multiplicative:
). Under uniform conditions, the
amount of attenuation (in dB) is proportional to the distance
traveled; in other words, the attenuation factors for two successive
segments of a propagation path are multiplicative: