| (B.40) | |||
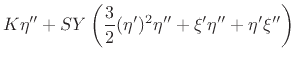 |
(B.41) | ||
| (B.42) |
The physical forward momentum carried by a transverse wave along a string is conveyed by a secondary longitudinal wave [394].
A less simplified wave equation which
supports longitudinal wave momentum is given by [394, Eqns. 38ab]
| (B.40) | |||
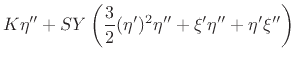 |
(B.41) | ||
| (B.42) |
| (B.43) | |||
| (B.44) |
Physically, the rising edge of a transverse wave generates a longitudinal displacement in the direction of wave travel that propagates ahead at a much higher speed (typically an order of magnitude faster). The falling edge of the transverse wave then cancels this forward displacement as it passes by. See [394] for further details (including computer simulations).