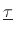Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Figure B.7:
Application of torque 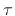 about the
origin given by a tangential force
about the
origin given by a tangential force 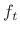 on a lever arm of length
on a lever arm of length
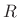 .
.
![\includegraphics[width=1.1in]{eps/torque}](img2941.png) |
When twisting things, the rotational force we apply about the center
is called a torque (or moment, or moment of
force). Informally, we think of the torque as the tangential
applied force 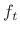 times the moment arm (length of the
lever arm)
times the moment arm (length of the
lever arm) 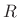
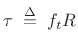 |
(B.26) |
as depicted in Fig.B.7. The moment arm is the distance from the
applied force to the point being twisted. For example, in the case of
a wrench turning a bolt, 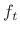 is the force applied at the end of the
wrench by one's hand, orthogonal to the wrench, while the moment arm
is the force applied at the end of the
wrench by one's hand, orthogonal to the wrench, while the moment arm
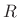 is the length of the wrench. Doubling the length of the wrench
doubles the torque. This is an example of leverage. When
is the length of the wrench. Doubling the length of the wrench
doubles the torque. This is an example of leverage. When 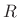 is increased, a given twisting angle
is increased, a given twisting angle 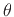 is spread out over a
larger arc length
is spread out over a
larger arc length 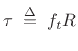 , thereby reducing the tangential force
, thereby reducing the tangential force
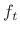 required to assert a given torque
required to assert a given torque 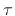 .
.
For more general applied forces
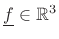 , we may compute the
tangential component
, we may compute the
tangential component
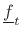 by projecting
by projecting
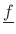 onto the
tangent direction. More precisely, the torque
onto the
tangent direction. More precisely, the torque 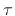 about the
origin
about the
origin
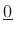 applied at a point
applied at a point
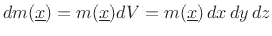 may be defined by
may be defined by
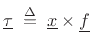 |
(B.27) |
where
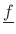 is the applied force (at
is the applied force (at
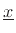 ) and
) and 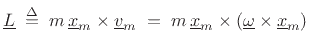 denotes the
cross product, introduced above in §B.4.12.
denotes the
cross product, introduced above in §B.4.12.
Note that the torque vector
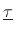 is orthogonal to both the lever
arm and the tangential-force direction. It thus points in the
direction of the angular velocity vector (along the axis of rotation).
is orthogonal to both the lever
arm and the tangential-force direction. It thus points in the
direction of the angular velocity vector (along the axis of rotation).
The torque magnitude is
where 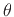 denotes the angle from
denotes the angle from
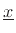 to
to
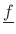 . We can
interpret
. We can
interpret
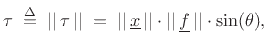 as the length of the projection of
as the length of the projection of
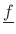 onto the tangent direction (the line orthogonal to
onto the tangent direction (the line orthogonal to
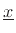 in the
direction of the force), so that we can write
in the
direction of the force), so that we can write
where
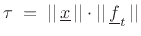 , thus getting back
to Eq.(B.26).
, thus getting back
to Eq.(B.26).
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![\includegraphics[width=1.1in]{eps/torque}](img2941.png)
![\includegraphics[width=1.1in]{eps/torque}](img2941.png)
![]() times the moment arm (length of the
lever arm)
times the moment arm (length of the
lever arm) ![]()
![]() , we may compute the
tangential component
, we may compute the
tangential component
![]() by projecting
by projecting
![]() onto the
tangent direction. More precisely, the torque
onto the
tangent direction. More precisely, the torque ![]() about the
origin
about the
origin
![]() applied at a point
applied at a point
![]() may be defined by
may be defined by
![]() is orthogonal to both the lever
arm and the tangential-force direction. It thus points in the
direction of the angular velocity vector (along the axis of rotation).
is orthogonal to both the lever
arm and the tangential-force direction. It thus points in the
direction of the angular velocity vector (along the axis of rotation).