Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Recall (§B.3) that the momentum of a mass  traveling
with velocity
traveling
with velocity  in a straight line is given by
in a straight line is given by
while the angular momentum of a point-mass  rotating along a circle
of radius
rotating along a circle
of radius 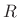 at
at 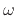 rad/s is given by
rad/s is given by
where 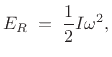 .
The tangential speed of the mass along the circle of radius
.
The tangential speed of the mass along the circle of radius 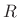 is given by
is given by
Expressing the angular momentum 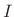 in terms of
in terms of  gives
gives
 |
(B.18) |
Thus, the angular momentum  is
is 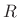 times the linear momentum
times the linear momentum
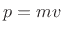 .
.
Linear momentum can be viewed as a renormalized special case of
angular momentum in which the radius of rotation goes to infinity.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() traveling
with velocity
traveling
with velocity ![]() in a straight line is given by
in a straight line is given by