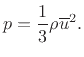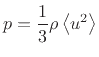
According the kinetic theory of ideal gases [181], air pressure can be defined as the average momentum transfer per unit area per unit time due to molecular collisions between a confined gas and its boundary. Using Newton's second law, this pressure can be shown to be given by one third of the average kinetic energy of molecules in the gas.
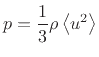
Here,
Proof: This is a classical result from the kinetic theory of gases
[181]. Let ![]() be the total mass of a gas
confined to a rectangular volume
be the total mass of a gas
confined to a rectangular volume ![]() , where
, where ![]() is the area of
one side and
is the area of
one side and ![]() the distance to the opposite side. Let
the distance to the opposite side. Let
![]() denote the average molecule velocity in the
denote the average molecule velocity in the ![]() direction. Then the
total net molecular momentum in the
direction. Then the
total net molecular momentum in the ![]() direction is given by
direction is given by
![]() . Suppose the momentum
. Suppose the momentum
![]() is directed
against a face of area
is directed
against a face of area ![]() . A rigid-wall elastic collision by a mass
. A rigid-wall elastic collision by a mass
![]() traveling into the wall at velocity
traveling into the wall at velocity
![]() imparts a momentum of
magnitude
imparts a momentum of
magnitude
![]() to the wall (because the momentum of the mass is
changed from
to the wall (because the momentum of the mass is
changed from
![]() to
to
![]() , and momentum is conserved).
The average momentum-transfer per unit area is therefore
, and momentum is conserved).
The average momentum-transfer per unit area is therefore
![]() at any instant in time. To obtain the definition of pressure, we need
only multiply by the average collision rate, which is given by
at any instant in time. To obtain the definition of pressure, we need
only multiply by the average collision rate, which is given by
![]() . That is, the average
. That is, the average ![]() -velocity divided by the
round-trip distance along the
-velocity divided by the
round-trip distance along the ![]() dimension gives the collision rate
at either wall bounding the
dimension gives the collision rate
at either wall bounding the ![]() dimension. Thus, we obtain
dimension. Thus, we obtain
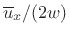
where
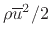 is the average molecular
velocity magnitude of the gas. Since the gas pressure must be the
same in all directions, by symmetry, we must have
is the average molecular
velocity magnitude of the gas. Since the gas pressure must be the
same in all directions, by symmetry, we must have