Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In summary, the following pointers can be offered regarding nonlinear
elements in a digital waveguide model:
- Verify that aliasing can be heard and sounds bad before working
to get rid of it.
- Aliasing (bandwidth expansion) is reduced by smoothing
``corners'' in the nonlinearity.
- Consider an oversampling factor for nonlinear
subsystems sufficient to accommodate the bandwidth expansion
caused by the nonlinearity.
- Make sure there is adequate lowpass filtering in a feedback loop
containing a nonlinearity.
As a specific example, consider the cubic nonlinearity used in a
feedback loop (as in §9.1.6). This can be done with
no aliasing at low levels (i.e., at levels below hard
clipping) provided we use
To avoid  oversampling in the entire feedback loop, we may
downsample by 3 after the lowpass filter and upsample by 3 just before
the nonlinearity. If the lowpass filter is good, the downsampling by
3 is trivially accomplished by throwing away every 2 out of 3 samples.
For upsampling, however, an additional third-band lowpass-filter is
needed for the interpolation (§4.4).
oversampling in the entire feedback loop, we may
downsample by 3 after the lowpass filter and upsample by 3 just before
the nonlinearity. If the lowpass filter is good, the downsampling by
3 is trivially accomplished by throwing away every 2 out of 3 samples.
For upsampling, however, an additional third-band lowpass-filter is
needed for the interpolation (§4.4).
A more agressive antialiasing scheme is to oversample by
only two (or between 2 and 3) for cubic nonlinearities, in
which case there is aliasing in the transition band, but it does not
reach the passband. More generally, for an 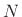 th-order nonlinearity,
oversampling by
th-order nonlinearity,
oversampling by  suffices to keep aliasing out of the passband.
This is a reasonable choice when the passband is the full audio band,
or (using a bit more oversampling) when the lowpass filter is high
order.
suffices to keep aliasing out of the passband.
This is a reasonable choice when the passband is the full audio band,
or (using a bit more oversampling) when the lowpass filter is high
order.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() th-order nonlinearity,
oversampling by
th-order nonlinearity,
oversampling by ![]() suffices to keep aliasing out of the passband.
This is a reasonable choice when the passband is the full audio band,
or (using a bit more oversampling) when the lowpass filter is high
order.
suffices to keep aliasing out of the passband.
This is a reasonable choice when the passband is the full audio band,
or (using a bit more oversampling) when the lowpass filter is high
order.