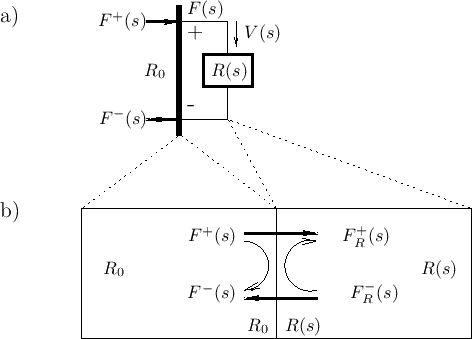
 |
Points to note:
- The infinitesimal waveguide is terminated by the element.
The element reflects waves as if it were a new waveguide section at
impedance
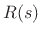 , as depicted in Fig.F.1b.
, as depicted in Fig.F.1b.
- The interface to the element is recast as traveling-wave
components
 and
and 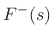 at impedance
at impedance 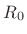 .
In terms of these components, the physical force on the element is
obtained by adding them together:
.
In terms of these components, the physical force on the element is
obtained by adding them together:
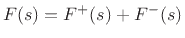 .
.
- The waveguide impedance
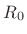 is arbitrary because it
has been physically introduced. We will need to know it when we
connect this element to other elements. The element's interface to
other elements is now a waveguide (transmission line) at real
impedance
is arbitrary because it
has been physically introduced. We will need to know it when we
connect this element to other elements. The element's interface to
other elements is now a waveguide (transmission line) at real
impedance 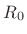 .
.
- The junction is ``parallel'' (cf. §7.2):
- Force (voltage) must be continuous across the junction, since
otherwise there would be a finite force across a zero mass, producing
infinite acceleration.
- The sum of velocities (currents) into the junction must be zero
by conservation of mass (charge).
- Force (voltage) must be continuous across the junction, since
otherwise there would be a finite force across a zero mass, producing
infinite acceleration.