Similarly, given any filter realization of the load admittance
![]() , we can split
, we can split ![]() into its
instantaneous and delayed components as
into its
instantaneous and delayed components as
![]() , and analogously obtain
, and analogously obtain
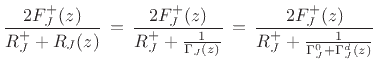 |
(C.123) | ||
![$\displaystyle \frac{2F_J^+(z)}{R_J^+ + \frac{1/\Gamma_J^0}{1 + \Gamma_J^d(z)/\Gamma_J^0}}
\,\mathrel{\mathop=}\,\frac{2F_J^+(z)}{R_J^+ + \frac{1}{\Gamma_J^0} + \frac{1}{\Gamma_J^0}\left[\frac{1}{1 + \Gamma_J^d(z)/\Gamma_J^0} - 1\right]}$](img4028.png) |
(C.124) | ||
![$\displaystyle \frac{2F_J^+(z)}{R_0 + \frac{1}{\Gamma_J^0}\left[\frac{-\Gamma_J^d(z)/\Gamma_J^0}{1+\Gamma_J^d(z)/\Gamma_J^0}\right]}
\,\mathrel{\mathop=}\,\frac{2F_J^+(z)/R_0}{1 + \frac{1}{R_0\Gamma_J^0}\left[\frac{-\Gamma_J^d(z)/\Gamma_J^0}{1+\Gamma_J^d(z)/\Gamma_J^0}\right]}$](img4029.png) |
(C.125) |
![\includegraphics[width=0.8\twidth]{eps/SeriesJunctionAdmittanceBiquads}](img4035.png) |
Figure C.31 can readily be encoded in the FAUST language by extracting a unit-sample delay
from the admittance filter and ``pushing'' it to the right through its
input summer, which splits it into the ![]() output tap and the inner
feedback loop. This makes both feedback loops valid in FAUST using
the tilde (`~') operator. In terms of obvious definitions:
output tap and the inner
feedback loop. This makes both feedback loops valid in FAUST using
the tilde (`~') operator. In terms of obvious definitions:
vJ = fJp : *(2*G0) : ( + ~
( *(G0/GJ0) : ( + : GJd/GJ0 : *(-1)) ~ _ : *(-1)));
where the delay in GJd has been pulled out:
GJd = _ <: par(i, M, GiJd(i+1)) :> _ ; GiJd(i) = fi.tf2(b1d(i), b2d(i), 0, a1(i), a2(i) ); // SHIFTED