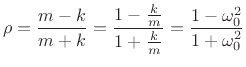Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
From Fig.F.35, we can see that the impedance of the parallel
combination of the mass and spring is given by
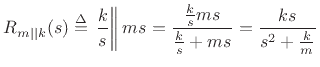 |
(F.55) |
(using the product-over-sum rule for combining impedances in
parallel). The poles of this impedance are given by the roots of the
denominator polynomial in 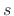 :
:
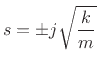 |
(F.56) |
The resonance frequency of the mass-spring oscillator is therefore
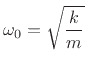 |
(F.57) |
Since the poles
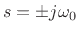 are on the
are on the  axis, there is
no damping, as we expect.
axis, there is
no damping, as we expect.
We can now write reflection coefficient 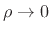 (see Fig.F.37) as
(see Fig.F.37) as
We see that dc (
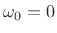 ) corresponds to
) corresponds to 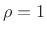 , and
, and
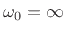 corresponds to
corresponds to 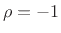 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
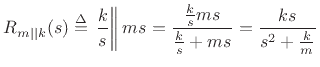
![]() (see Fig.F.37) as
(see Fig.F.37) as