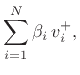 |
(F.45) | ||
| (F.46) |
As we saw for the parallel case in §F.2.3, the series three-port adaptor (scattering junction) with reflection-free port can be implemented using only one multiply.
The scattering relations in terms of the beta parameters introduced in §F.2.5 for a series junction
of any number of ports:
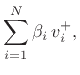 |
(F.45) | ||
| (F.46) |
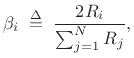
and
As for the parallel case, we set ![]() ,
, ![]() ,
, ![]() , and
, and
![]() . With port A reflection-free, we have
. With port A reflection-free, we have
![]() .
Dividing all impedances by
.
Dividing all impedances by ![]() gives
gives ![]() , and
, and
![]() . Our one degree of freedom may be chosen as
. Our one degree of freedom may be chosen as
![]() , and then
, and then
![]() .
.
The beta parameters become ![]() ,
,
![]() , and
, and
![]() , so that the scattering formulas are
, so that the scattering formulas are
| (F.47) | |||
| (F.48) |
| (F.49) | |||
| (F.50) | |||
| (F.51) | |||
| (F.52) | |||
| (F.53) | |||
| (F.54) |
The series adaptor has now been derived in a way which emphasizes its duality with respect to the parallel adaptor.