Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
For ideal numerical scaling in the 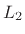 sense, we may choose to propagate
normalized waves which lead to normalized scattering junctions
analogous to those encountered in normalized ladder filters [299].
Normalized waves may be either normalized pressure
sense, we may choose to propagate
normalized waves which lead to normalized scattering junctions
analogous to those encountered in normalized ladder filters [299].
Normalized waves may be either normalized pressure
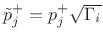 or normalized velocity
or normalized velocity
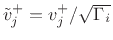 . Since the signal power associated with a traveling
wave is simply
. Since the signal power associated with a traveling
wave is simply
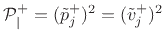 ,
they may also be called root-power waves [436].
Appendix C develops this topic in more detail.
,
they may also be called root-power waves [436].
Appendix C develops this topic in more detail.
The scattering matrix for normalized pressure waves is given by
![$\displaystyle \tilde{\mathbf{A}}= \left[ \begin{array}{llll} \frac{2 \Gamma_{1}}{\Gamma_J} - 1 & \frac{2 \sqrt{\Gamma_{1}\Gamma_{2}}}{\Gamma_J} & \dots & \frac{2 \sqrt{\Gamma_{1}\Gamma_{n}}}{\Gamma_J} \\ \\ \frac{2 \sqrt{\Gamma_{2}\Gamma_{1}}}{\Gamma_J} & \frac{2 \Gamma_{2}}{\Gamma_J}-1 & \dots & \frac{2 \sqrt{\Gamma_{2}\Gamma_{n}}}{\Gamma_J} \\ \dots & & \dots\\ \dots & & \dots\\ \frac{2 \sqrt{\Gamma_{n}\Gamma_{1}}}{\Gamma_J} & \frac{2 \sqrt{\Gamma_{n}\Gamma_{2}}}{\Gamma_J} & \dots & \frac{2 \Gamma_{n}}{\Gamma_J} -1 \end{array} \right]$](img4137.png) |
(C.143) |
The normalized scattering matrix can be expressed as a negative Householder reflection
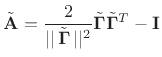 |
(C.144) |
where
![$ \tilde{{\bm \Gamma}}^T= [\sqrt{\Gamma_1},\ldots,\sqrt{\Gamma_N}]$](img4139.png) , and
, and
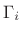 is the wave admittance in the
is the wave admittance in the 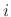 th waveguide branch. To
eliminate the sign inversion, the reflections at the far end of each
waveguide can be chosen as -1 instead of 1. The geometric
interpretation of (C.145) is that the incoming pressure waves are
reflected about the vector
th waveguide branch. To
eliminate the sign inversion, the reflections at the far end of each
waveguide can be chosen as -1 instead of 1. The geometric
interpretation of (C.145) is that the incoming pressure waves are
reflected about the vector
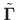 . Unnormalized scattering junctions
can be expressed in the form of an ``oblique'' Householder reflection
. Unnormalized scattering junctions
can be expressed in the form of an ``oblique'' Householder reflection
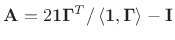 , where
, where
![$ \mathbf{1}^T=[1,\ldots,1]$](img4143.png) and
and
![$ {\bm \Gamma}^T= [\Gamma_1,\ldots,\Gamma_N]$](img4144.png) .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() sense, we may choose to propagate
normalized waves which lead to normalized scattering junctions
analogous to those encountered in normalized ladder filters [299].
Normalized waves may be either normalized pressure
sense, we may choose to propagate
normalized waves which lead to normalized scattering junctions
analogous to those encountered in normalized ladder filters [299].
Normalized waves may be either normalized pressure
![]() or normalized velocity
or normalized velocity
![]() . Since the signal power associated with a traveling
wave is simply
. Since the signal power associated with a traveling
wave is simply
![]() ,
they may also be called root-power waves [436].
Appendix C develops this topic in more detail.
,
they may also be called root-power waves [436].
Appendix C develops this topic in more detail.