Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In the musical acoustics literature, the normal method for creating a
computational model from a differential equation is to apply the
so-called finite difference approximation (FDA) in which
differentiation is replaced by a finite difference (see Appendix D)
[484,314]. For example
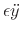 |
(C.2) |
and
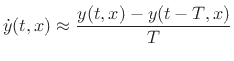 |
(C.3) |
where  is the time sampling interval to be used in the simulation, and
is the time sampling interval to be used in the simulation, and
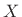 is a spatial sampling interval. These approximations can be seen as
arising directly from the definitions of the partial derivatives with
respect to
is a spatial sampling interval. These approximations can be seen as
arising directly from the definitions of the partial derivatives with
respect to 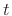 and
and  . The approximations become exact in the limit as
. The approximations become exact in the limit as
 and
and 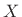 approach zero. To avoid a delay error, the second-order
finite-differences are defined with a compensating time shift:
approach zero. To avoid a delay error, the second-order
finite-differences are defined with a compensating time shift:
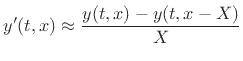 |
(C.4) |
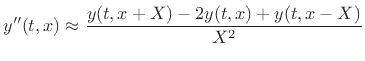 |
(C.5) |
The odd-order derivative approximations suffer a half-sample delay error
while all even order cases can be compensated as above.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]