Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Delay Operator Notation
It is convenient to think of the FDA in terms of time-domain
difference operators using a delay operator notation. The
delay operator  is defined by
is defined by
Thus, the first-order difference (derivative approximation) is
represented in the time domain by 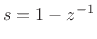 . We can think of
. We can think of  as
as
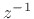 since, by the shift theorem for
since, by the shift theorem for 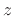 transforms,
transforms,
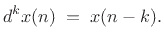 is the
is the 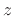 transform of
transform of  delayed (right shifted) by
delayed (right shifted) by 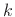 samples.
samples.
The obvious definition for the second derivative is
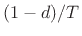 |
(8.4) |
However, a better definition is the centered finite difference
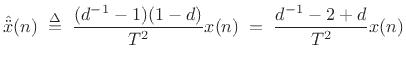 |
(8.5) |
where 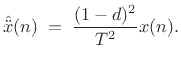 denotes a unit-sample advance. This definition
is preferable as long as one sample of look-ahead is available, since
it avoids an operator delay of one sample. Equation (7.5) is a
zero phase filter, meaning it has no delay at any frequency,
while (7.4) is a linear phase filter having a delay of
denotes a unit-sample advance. This definition
is preferable as long as one sample of look-ahead is available, since
it avoids an operator delay of one sample. Equation (7.5) is a
zero phase filter, meaning it has no delay at any frequency,
while (7.4) is a linear phase filter having a delay of
 sample at all frequencies.
sample at all frequencies.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() is defined by
is defined by