Striking One of the Masses

Now let $f(t,x) = \delta(t)\delta(x-r)$ . That is, we apply an impulse of vertical momentum to the mass on the right at time 0 .

In this case, the unit of vertical momentum is transferred entirely to the mass on the right, so that

$$p \eqsp 1 \eqsp m v_r \,\,\Rightarrow\,\,v_r \eqsp \frac{1}{m},$$

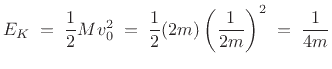
which is twice as fast as before. Just after time zero, we have $v_r=1/m$ , $v_{-r}=0$ , and, because the massless rod remains rigid, $v_0=1/(2m)$ .

Note that the velocity of the center-of-mass $1/(2m)$ is the same as it was when we hit the midpoint of the rod. This is an important general equivalence: The sum of all external force vectors acting on a rigid body can be applied as a single resultant force vector to the total mass concentrated at the center of mass to find the linear (translational) motion produced. (Recall from §B.4.1 that such a sum is the same as the sum of all radially acting external force components, since the tangential components contribute only to rotation and not to translation.)

All of the kinetic energy is in the mass on the right just after time zero:

$$E_K \eqsp \frac{1}{2}mv_r^2 \eqsp \frac{1}{2}m\left(\frac{1}{m}\right)^2 \eqsp \frac{1}{2m} \protect$$ (B.13)

However, after time zero, things get more complicated, because the mass on the left gets dragged into a rotation about the center of mass.

To simplify ongoing analysis, we can define a body-fixed frame of reference^B.16 having its origin at the center of mass. Let $v'$ denote a velocity in this frame. Since the velocity of the center of mass is $v_0=1/(2m)$ , we can convert any velocity $v'$ in the body-fixed frame to a velocity $v$ in the original frame by adding $v_0$ to it, viz.,

$$v \eqsp v' + v_0 \eqsp v' + \frac{1}{2m}.$$

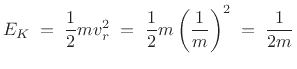
The mass velocities in the body-fixed frame are now

$$v'_{-r} \eqsp -\frac{1}{2m},\qquad\qquad v'_r \eqsp \frac{1}{2m},$$

and of course $v'_0=0$ .

In the body-fixed frame, all kinetic energy is rotational about the origin. Recall (Eq.(B.9)) that the moment of inertia for this system, with respect to the center of mass at $x=0$ , is

$$I \eqsp m(-r)^2 + m r^2 \eqsp 2mr^2.$$

Thus, the rotational kinetic energy (§B.4.3) is found to be

$$E'_R \eqsp \frac{1}{2}I\omega^2 \eqsp \frac{1}{2}(2mr^2)\left(\frac{v'_r}{r}\right)^2 \eqsp mr^2\left(\frac{1}{2mr}\right)^2 \eqsp \frac{1}{4m}.$$

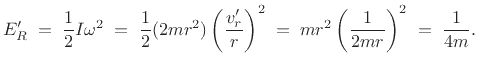
This is half of the kinetic energy we computed in the original ``space-fixed'' frame (Eq.(B.13) above). The other half is in the translational kinetic energy not seen in the body-fixed frame. As we saw in §B.4.2 above, we can easily calculate the translational kinetic energy as that of the total mass $M=2m$ traveling at the center-of-mass velocity $v_0=1/(2m)$ :

$$E'_K \eqsp \frac{1}{2}Mv_0^2 \eqsp \frac{1}{2}(2m)\left(\frac{1}{2m}\right)^2 \eqsp \frac{1}{4m}$$

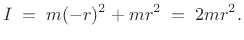
Adding this translational kinetic energy to the rotational kinetic energy in the body-fixed frame yields the total kinetic energy, as it must.

In summary, we defined a moving body-fixed frame having its origin at the center-of-mass, and the total kinetic energy was computed to be

$$E_K \eqsp E'_K + E'_R \eqsp \frac{1}{4m} + \frac{1}{4m} \eqsp \frac{1}{2m}$$

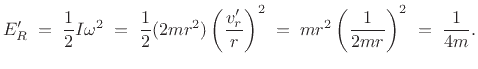
in agreement with the more complicated (after time zero) space-fixed analysis in Eq.(B.13).

It is important to note that, after time zero, both the linear momentum of the center-of-mass ( $p_0=Mv_0=(2m)(v_r/2) = mv_r=m\cdot(1/(2m))=1/2$ ), and the angular momentum in the body-fixed frame ( $L'=I\omega= (2mr^2)(v'_r/r)=(2mr^2)(1/(2mr))=r/2$ ) remain constant over time.^B.17 In the original space-fixed frame, on the other hand, there is a complex transfer of momentum back and forth between the masses after time zero.

Similarly, the translational kinetic energy of the total mass, treated as being concentrated at its center-of-mass, and the rotational kinetic energy in the body-fixed frame, are both constant after time zero, while in the space-fixed frame, kinetic energy transfers back and forth between the two masses. At all times, however, the total kinetic energy is the same in both formulations.