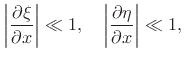Let's now assume the string is perfectly flexible (zero stiffness) so
that the direction of the force vector
![]() is given by the unit
vector
is given by the unit
vector
![]() tangent to the string. (To accommodate
stiffness, it would be necessary to include a force component at right
angles to the string which depends on the curvature and stiffness of
the string.) The magnitude of
tangent to the string. (To accommodate
stiffness, it would be necessary to include a force component at right
angles to the string which depends on the curvature and stiffness of
the string.) The magnitude of
![]() at any position is the rest
tension
at any position is the rest
tension ![]() plus the incremental tension needed to stretch it the
fractional amount
plus the incremental tension needed to stretch it the
fractional amount
If
so that
The four equations (B.31) through (B.35) can be combined into a single vector wave equation that expresses the propagation of waves on the string having three displacement components. This differential equation is nonlinear, so that superposition no longer holds. Furthermore, the three displacement components of the wave are coupled together at all points along the string, so that the wave equation is no longer separable into three independent 1D wave equations.
To obtain a linear, separable wave equation, it is necessary to assume
that the strains
![]() ,
,
![]() , and
, and
![]() be
small compared with unity. This is the same assumption
(
be
small compared with unity. This is the same assumption
(
![]() ) necessary to derive the
usual wave equation for transverse vibrations only in the
) necessary to derive the
usual wave equation for transverse vibrations only in the ![]() -
-![]() plane.
plane.
When (B.35) is expanded into a Taylor series in the strains (see (B.33)), and when only the first-order terms are retained, we obtain
 |
(B.36) |
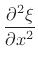 |
(B.37) | ||
 |
(B.38) | ||
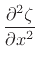 |
(B.39) |
In summary, the two transverse wave components and the longitudinal component may be considered independent (i.e., ``superposition'' holds with respect to vibrations in these three dimensions of vibration) provided powers higher than 1 of the strains (relative displacement) can be neglected, i.e.,
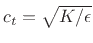 and
and