Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Newton's second law ``force equals mass times acceleration'' implies that
the pressure gradient in a gas is proportional to the acceleration of a
differential volume element in the gas. Let 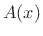 denote the area of the
surface of constant phase at radial coordinate
denote the area of the
surface of constant phase at radial coordinate  in the tube. Then the
total force acting on the surface due to pressure is
in the tube. Then the
total force acting on the surface due to pressure is
 , as
shown in Fig.C.47.
, as
shown in Fig.C.47.
Figure C.47:
Differential volume element for the conical acoustic tube.
![\includegraphics[width=3in]{eps/fconic}](img4335.png) |
The net force 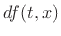 to the right across the volume element
between
to the right across the volume element
between  and
and 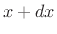 is then
is then
where, when time and/or position arguments have been dropped, as in
the last line above, they are all understood to be 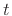 and
and  ,
respectively. To apply Newton's second law equating net force to mass
times acceleration, we need the mass of the volume element
,
respectively. To apply Newton's second law equating net force to mass
times acceleration, we need the mass of the volume element
where 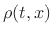 denotes air density.
denotes air density.
The center-of-mass acceleration of the volume element can be written
as
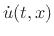 where
where 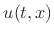 is particle velocity.C.20 Applying Newton's second law
is particle velocity.C.20 Applying Newton's second law
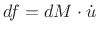 , we
obtain
, we
obtain
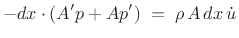 |
(C.167) |
or, dividing through by 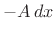 ,
,
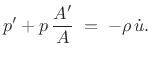 |
(C.168) |
In terms of the logarithmic derivative of 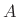 , this can be written
, this can be written
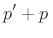 ln ln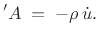 |
(C.169) |
Note that 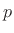 denotes small-signal acoustic pressure, while
denotes small-signal acoustic pressure, while
 denotes the full gas density (not just an acoustic perturbation
in the density). We may therefore treat
denotes the full gas density (not just an acoustic perturbation
in the density). We may therefore treat  as a constant.
as a constant.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote the area of the
surface of constant phase at radial coordinate
denote the area of the
surface of constant phase at radial coordinate ![]() in the tube. Then the
total force acting on the surface due to pressure is
in the tube. Then the
total force acting on the surface due to pressure is
![]() , as
shown in Fig.C.47.
, as
shown in Fig.C.47.
![]() to the right across the volume element
between
to the right across the volume element
between ![]() and
and ![]() is then
is then
![\begin{eqnarray*}
dM(t,x) &=& \int_x^{x+dx} \rho(t,\xi) A(\xi)\,d\xi \\ [5pt]
&\approx& \int_x^{x+dx} \left[\rho(t,x)+\rho'(t,x)(\xi-x)][A(x)+A'(x)(\xi-x)\right]d\xi\\ [5pt]
&\approx& \rho(t,x) A(x)\,dx + \int_x^{x+dx} \left[\rho'(t,x)A(x)+\rho(t,x)A'(x)\right](\xi-x)\,d\xi\\ [5pt]
&=& \rho\,A\,dx + \left(\rho' A+\rho A' \right)\frac{(dx)^2}{2}\\ [5pt]
&\approx& \rho\, A\,dx,
\end{eqnarray*}](img4343.png)
![]() denotes air density.
denotes air density.
![]() where
where ![]() is particle velocity.C.20 Applying Newton's second law
is particle velocity.C.20 Applying Newton's second law
![]() , we
obtain
, we
obtain