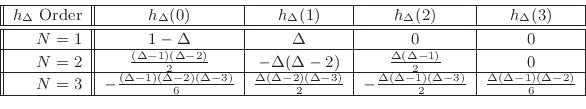Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Explicit Lagrange Coefficient Formulas
Given a desired fractional delay of 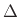 samples, the Lagrange
fraction-delay impulse response can be written in closed form as
samples, the Lagrange
fraction-delay impulse response can be written in closed form as
 |
(5.7) |
The following table gives specific examples for orders 1, 2, and 3:
Note that, for 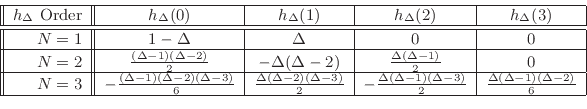 , Lagrange
interpolation reduces to linear interpolation, i.e., the
interpolator impulse response is
, Lagrange
interpolation reduces to linear interpolation, i.e., the
interpolator impulse response is
![$ h = [1-\Delta,\Delta]$](img1037.png) . Also,
remember that, for order
. Also,
remember that, for order 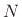 , the desired delay should be in a
one-sample range centered about
, the desired delay should be in a
one-sample range centered about
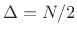 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() samples, the Lagrange
fraction-delay impulse response can be written in closed form as
samples, the Lagrange
fraction-delay impulse response can be written in closed form as