Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Considering the dc case first ( ), we see from Fig.F.37
that the state variable
), we see from Fig.F.37
that the state variable  will circulate unchanged in the
isolated loop on the left. Let's call this value
will circulate unchanged in the
isolated loop on the left. Let's call this value
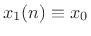 . Then the physical force on the spring is always equal to
. Then the physical force on the spring is always equal to
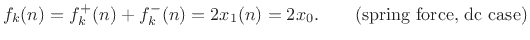 |
(F.58) |
The loop on the right in Fig.F.37 receives 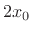 and adds
and adds
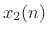 to that. Since
to that. Since
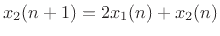 , we see it is
linearly growing in amplitude. For example, if
, we see it is
linearly growing in amplitude. For example, if 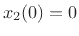 (with
(with
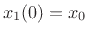 ), we obtain
), we obtain
![$ x_2=[0, 2x_0, 4x_0, 6x_0,\ldots]$](img5120.png) , or
, or
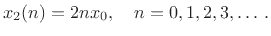 |
(F.59) |
At first, this result might appear to contradict conservation of
energy, since the state amplitude seems to be growing without bound.
However, the physical force is fortunately better behaved:
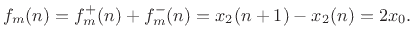 |
(F.60) |
Since the spring and mass are connected in parallel, it must be the
true that they are subjected to the same physical force at all times.
Comparing Equations (F.58-F.60) verifies this to be the case.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() ), we see from Fig.F.37
that the state variable
), we see from Fig.F.37
that the state variable ![]() will circulate unchanged in the
isolated loop on the left. Let's call this value
will circulate unchanged in the
isolated loop on the left. Let's call this value
![]() . Then the physical force on the spring is always equal to
. Then the physical force on the spring is always equal to