The center of mass (or centroid) of a rigid body is
found by averaging the spatial points of the body
![]() weighted by the mass
weighted by the mass ![]() of those points:B.12
of those points:B.12
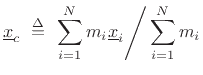
Thus, the center of mass is the mass-weighted average location of the object. For a continuous mass distribution totaling up to
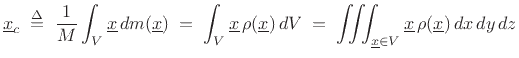
where the volume integral is taken over a volume
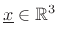
A nice property of the center of mass is that gravity acts on a far-away object as if all its mass were concentrated at its center of mass. For this reason, the center of mass is often called the center of gravity.