Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Beta Parameters
It is customary in the wave digital filter literature to define the
beta parameters
as
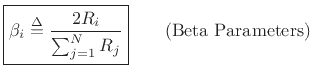 |
(F.33) |
where 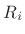 are the port impedances (attached element reference
impedances). In terms of the beta parameters, the force-wave series
adaptor performs the following computations:
are the port impedances (attached element reference
impedances). In terms of the beta parameters, the force-wave series
adaptor performs the following computations:
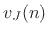 |
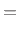 |
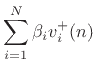 (Common Junction Velocity) (Common Junction Velocity)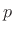 |
(F.34) |
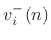 |
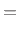 |
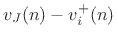 (Outgoing Velocity Waves) (Outgoing Velocity Waves)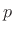 |
(F.35) |
However, we normally employ a mixture of parallel and series adaptors,
while keeping a force-wave simulation. Since
 , we obtain, after a small amount of algebra, the following
recipe for the series force-wave adaptor:
, we obtain, after a small amount of algebra, the following
recipe for the series force-wave adaptor:
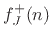 |
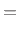 |
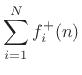 (Total Incoming Force) (Total Incoming Force)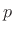 |
(F.36) |
 |
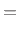 |
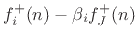 (Outgoing Force Waves) (Outgoing Force Waves)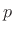 |
(F.37) |
We see that we have 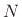 multiplies and
multiplies and  additions as in the
parallel-adaptor case.
additions as in the
parallel-adaptor case.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
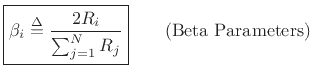
![]() , we obtain, after a small amount of algebra, the following
recipe for the series force-wave adaptor:
, we obtain, after a small amount of algebra, the following
recipe for the series force-wave adaptor: