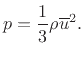Bernoulli Equation

In an ideal inviscid, incompressible flow, we have, by conservation of energy,

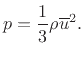$$p + \frac{1}{2}\rho u^2 + \rho g h =$$   constant

where

$$\begin{eqnarray*} p &=& \mbox{pressure (newtons/m$^2$\ = kg /(m s$^2$))}\\ u &=& \mbox{particle velocity (m/s)}\\ \rho &=& \mbox{volume density of air (kg/m$^3$)}\\ g &=& \mbox{Newton's gravitational constant (m/s$^2$)}\\ h &=& \mbox{Height of flow's center-of-mass axis (m)}\\ \mbox{\lq\lq Inviscid''} &=& \mbox{\lq\lq Frictionless'', \lq\lq Lossless''} \end{eqnarray*}$$

This basic energy conservation law was published in 1738 by Daniel Bernoulli in his classic work Hydrodynamica.

From §B.7.3, we have that the pressure of a gas is proportional to the average kinetic energy of the molecules making up the gas. Therefore, when a gas flows at a constant height $h$ , some of its ``pressure kinetic energy'' must be given to the kinetic energy of the flow as a whole. If the mean height of the flow changes, then kinetic energy trades with potential energy as well.