Approximate Maximum Likelihood F0 Estimation

In applications for which the fundamental frequency F0 must be measured very accurately in a periodic signal, the estimate ${\hat f}_0$ obtained by the above algorithm can be refined using a gradient search which matches a so-called ``harmonic comb'' to the magnitude spectrum of an interpolated FFT $X(\omega)$ :

$${\hat f}_0 \isdefs \arg\max_{{\hat f}_0} \sum_{k=1}^K \log\left[\left\vert X(k{\hat f}_0)\right\vert+\epsilon\right] \eqsp \arg\max_{{\hat f}_0} \prod_{k=1}^K \left[\left\vert X(k{\hat f}_0)\right\vert+\epsilon\right]$$

where

$$\begin{eqnarray*} K &=& \mbox{number of peaks}\\ k &=& \mbox{harmonic number of $k$th peak (valid method for non-stiff strings)}\\ \epsilon &=& \mbox{small value on the order of spectral magnitude \emph{noise floor level}} \end{eqnarray*}$$

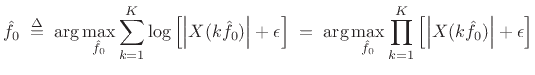
Note that freely vibrating strings are not exactly periodic due to exponenential decay, coupling effects, and stiffness (which stretches harmonics into quasiharmonic overtones, as explained in §6.9). However, non-stiff strings can often be analyzed as having approximately harmonic spectra ( $\leftrightarrow$ periodic time waveform) over a limited time frame.

Since string spectra typically exhibit harmonically spaced nulls associated with the excitation and/or observation points, as well as from other phenomena such as recording multipath and/or reverberation, it is advisable to restrict $K$ to a range that does not include any spectral nulls (or simply omit index $k$ when $k{\hat f}_0$ is too close to a spectral null), since even one spectral null can push the product of peak amplitudes to a very small value. As a practical matter, it is important to inspect the magnitude spectra of the data manually to ensure that a robust row of peaks is being matched by the harmonic comb. For example, a display of the frame magnitude spectrum overlaid with vertical lines at the optimized harmonic-comb frequencies yields an effective picture of the F0 estimate in which typical problems (such as octave errors) are readily seen.