Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
In a similar way, we can compute the signal energy
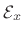 (sum of squared moduli) using any of the following constructs:
(sum of squared moduli) using any of the following constructs:
Ex = x(:)' * x(:)
Ex = sum(conj(x(:)) .* x(:))
Ex = sum(abs(x(:)).^2)
The average power (energy per sample) is similarly Px = Ex/N.
The
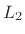 norm is similarly xL2 = sqrt(Ex) (same result as
xL2 = norm(x)). The
norm is similarly xL2 = sqrt(Ex) (same result as
xL2 = norm(x)). The
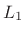 norm is given by xL1 =
sum(abs(x)) or by xL1 = norm(x,1). The infinity-norm
(Chebyshev norm) is computed as xLInf = max(abs(x)) or
xLInf = norm(x,Inf). In general,
norm is given by xL1 =
sum(abs(x)) or by xL1 = norm(x,1). The infinity-norm
(Chebyshev norm) is computed as xLInf = max(abs(x)) or
xLInf = norm(x,Inf). In general,
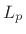 norm is computed by
norm(x,p), with p=2 being the default case.
norm is computed by
norm(x,p), with p=2 being the default case.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() (sum of squared moduli) using any of the following constructs:
(sum of squared moduli) using any of the following constructs: