Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Plotting Complex Sinusoids versus Frequency
As discussed in the previous section, we regard the signal
as a positive-frequency sinusoid when
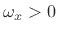 . In a
manner analogous to spectral magnitude plots (discussed in
§4.1.6), we can plot this complex sinusoid over a frequency
axis as a vertical line of length
. In a
manner analogous to spectral magnitude plots (discussed in
§4.1.6), we can plot this complex sinusoid over a frequency
axis as a vertical line of length 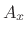 at the point
at the point
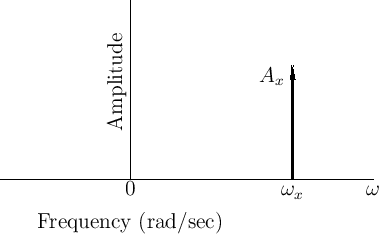
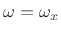 , as shown in Fig.4.10. Such a plot of
amplitude versus frequency may be called a spectral plot, or
spectral representation [46] of the (zero-phase)
complex sinusoid.
, as shown in Fig.4.10. Such a plot of
amplitude versus frequency may be called a spectral plot, or
spectral representation [46] of the (zero-phase)
complex sinusoid.
Figure 4.10:
Spectral plot of a complex sinusoid
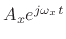 .
.
 |
More generally, however, a complex sinusoid has both an amplitude and
a phase (or, equivalently, a complex amplitude):
To accommodate the phase angle  in spectral plots, the
plotted vector may be rotated by the angle
in spectral plots, the
plotted vector may be rotated by the angle  in the plane
orthogonal to the frequency axis passing through
in the plane
orthogonal to the frequency axis passing through 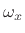 , as done
in Fig.4.16b below (p.
, as done
in Fig.4.16b below (p. ![[*]](../icons/crossref.png) )
for phase angles
)
for phase angles
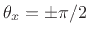 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]