Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
How should we define 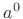 in a manner consistent with the
properties of integer exponents? Multiplying it by
in a manner consistent with the
properties of integer exponents? Multiplying it by 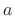 gives
gives
by property (1) of exponents. Solving
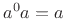 for
for 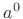 then
gives
then
gives
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() in a manner consistent with the
properties of integer exponents? Multiplying it by
in a manner consistent with the
properties of integer exponents? Multiplying it by ![]() gives
gives