Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Let 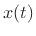 denote any continuous-time signal having a Fourier
Transform (FT)
denote any continuous-time signal having a Fourier
Transform (FT)
Let
denote the samples of 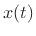 at uniform intervals of
at uniform intervals of 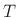 seconds,
and denote its Discrete-Time Fourier Transform (DTFT) by
seconds,
and denote its Discrete-Time Fourier Transform (DTFT) by
Then the spectrum 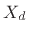 of the sampled signal
of the sampled signal 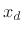 is related to the
spectrum
is related to the
spectrum 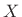 of the original continuous-time signal
of the original continuous-time signal 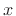 by
by
The terms in the above sum for 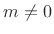 are called aliasing
terms. They are said to alias into the base band
are called aliasing
terms. They are said to alias into the base band
![$ [-\pi/T,\pi/T]$](img1783.png) . Note that the summation of a spectrum with
aliasing components involves addition of complex numbers; therefore,
aliasing components can be removed only if both their amplitude
and phase are known.
. Note that the summation of a spectrum with
aliasing components involves addition of complex numbers; therefore,
aliasing components can be removed only if both their amplitude
and phase are known.
Proof:
Writing 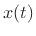 as an inverse FT gives
as an inverse FT gives
Writing 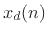 as an inverse DTFT gives
as an inverse DTFT gives
where
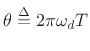 denotes the normalized discrete-time
frequency variable.
denotes the normalized discrete-time
frequency variable.
The inverse FT can be broken up into a sum of finite integrals, each of length
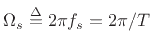 , as follows:
, as follows:
Let us now sample this representation for 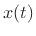 at
at 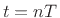 to obtain
to obtain
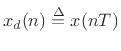 , and we have
, and we have
since  and
and 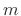 are integers.
Normalizing frequency as
are integers.
Normalizing frequency as
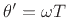 yields
yields
Since this is formally the inverse DTFT of
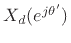 written in terms of
written in terms of
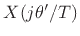 ,
the result follows.
,
the result follows.

Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote any continuous-time signal having a Fourier
Transform (FT)
denote any continuous-time signal having a Fourier
Transform (FT)
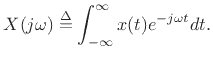
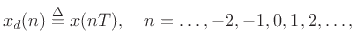
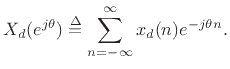
![$\displaystyle X_d(e^{j\theta}) = \frac{1}{T} \sum_{m=-\infty}^\infty X\left[j\left(\frac{\theta}{T}
+ m\frac{2\pi}{T}\right)\right].
$](img1781.png)
![]() as an inverse FT gives
as an inverse FT gives
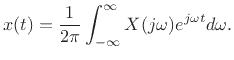
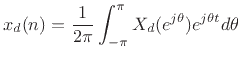
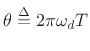 denotes the normalized discrete-time
frequency variable.
denotes the normalized discrete-time
frequency variable.
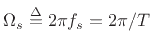 , as follows:
, as follows:
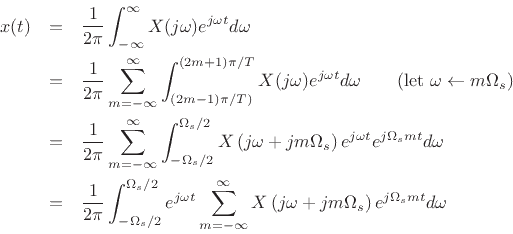
![]() at
at ![]() to obtain
to obtain
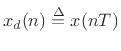 , and we have
, and we have
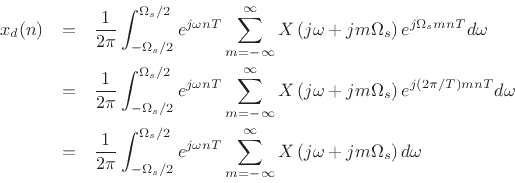
![]() and
and ![]() are integers.
Normalizing frequency as
are integers.
Normalizing frequency as
![]() yields
yields
![$\displaystyle x_d(n) = \frac{1}{2\pi}\int_{-\pi}{\pi} e^{j\theta^\prime n}
\frac{1}{T}\sum_{m=-\infty}^\infty X\left[j\left(\frac{\theta^\prime }{T}
+ m\frac{2\pi}{T}\right) \right] d\theta^\prime .
$](img1793.png)