Impedance

Impedance is defined for mechanical systems as force divided by velocity, while the inverse (velocity/force) is called an admittance. For dynamic systems, the impedance of a ``driving point'' is defined for each frequency $\omega$ , so that the ``force'' in the definition of impedance is best thought of as the peak amplitude of a sinusoidal applied force, and similarly for the velocity. Thus, if $F(\omega)$ denotes the Fourier transform of the applied force at a driving point, and $V(\omega)$ is the Fourier transform of the resulting velocity of the driving point, then the driving-point impedance is given by

$$R(\omega) \isdef \frac{F(\omega)}{V(\omega)}.$$

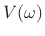
In the lossless case (no dashpots, only masses and springs), all driving-point impedances are purely imaginary, and a purely imaginary impedance is called a reactance. A purely imaginary admittance is called a susceptance. The term immittance refers to either an impedance or an admittance [35]. In mechanics, force is typically in units of newtons (kilograms times meters per second squared) and velocity is in meters per second.

In acoustics [320,321], force takes the form of pressure (e.g., in physical units of newtons per meter squared), and velocity may be either particle velocity in open air (meters per second) or volume velocity in acoustic tubes (meters cubed per second) (see §B.7.1 for definitions). The wave impedance (also called the characteristic impedance) in open air is the ratio of pressure to particle velocity in a sound wave traveling through air, and it is given by $R= \sqrt{\gamma P_0\rho } = \rho c$ , where $\rho$ is the density (mass per unit volume) of air, $c$ is the speed of sound propagation, $P_0$ is ambient pressure, and $\gamma_c = 1.4$ is the ratio of the specific heat of air at constant pressure to that at constant volume. In a vibrating string, the wave impedance is given by $R= \sqrt{K\epsilon }=\epsilon c$ , where $\epsilon$ is string density (mass per unit length) and $K$ is the tension of the string (stretching force), as discussed further in §C.1 and §B.5.2.

In circuit theory [110], force takes the form of electric potential in volts, and velocity manifests as electric current in amperes (coulombs per second). In an electric transmission line, the characteristic impedance is given by $R=\sqrt{L/C}$ , where $L$ and $C$ are the inductance and capacitance, respectively, per unit length along the transmission line. In free space, the wave impedance for light is $R=\sqrt{\mu_0/\epsilon_0} =\mu_0 c_l$ , where $c_l$ denotes the speed of light, and $\mu_0$ and $\epsilon_0$ are the permeability and permittivity, respectively, of free space. One might be led from this to believe that there must exist a medium, or ``ether'', which sustains wave propagation in free space; however, this is one instance in which ``obvious'' predictions from theory turn out to be wrong (see the special theory of relativity for details).