Real Exponents

The closest we can actually get to most real numbers is to compute a rational number that is as close as we need. It can be shown that rational numbers are dense in the real numbers; that is, between every two real numbers there is a rational number, and between every two rational numbers is a real number.^3.1An irrational number can be defined as any real number having a non-repeating decimal expansion. For example, $\sqrt{2}$ is an irrational real number whose decimal expansion starts out as^3.2

$$\sqrt{2} = 1.414213562373095048801688724209698078569671875376948073176679\dots$$

Every truncated, rounded, or repeating expansion is a rational number. That is, it can be rewritten as an integer divided by another integer. For example,

$$1.414 = \frac{1414}{1000}$$

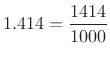
and, using $\overline{\mbox{overbar}}$ to denote the repeating part of a decimal expansion, a repeating example is as follows:

$$\begin{eqnarray*} x &=& 0.\overline{123} \\ [5pt] \quad\Rightarrow\quad 1000x &=& 123.\overline{123} = 123 + x\\ [5pt] \quad\Rightarrow\quad 999x &=& 123\\ [5pt] \quad\Rightarrow\quad x &=& \frac{123}{999} \end{eqnarray*}$$

Examples of irrational numbers include

$$\begin{eqnarray*} \pi &=& 3.1415926535897932384626433832795028841971693993751058209749\dots\\ e &=& 2.7182818284590452353602874713526624977572470936999595749669\dots\,. \end{eqnarray*}$$

Their decimal expansions do not repeat.

Let ${\hat x}_n$ denote the $n$ -digit decimal expansion of an arbitrary real number $x$ . Then ${\hat x}_n$ is a rational number (some integer over $10^n$ ). We can say

$$\lim_{n\to\infty} {\hat x}_n = x.$$

That is, the limit of ${\hat x}_n$ as $n$ goes to infinity is $x$ .

Since $a^{{\hat x}_n}$ is defined for all $n$ , we naturally define $a^x$ as the following mathematical limit:

$$\zbox {a^x \isdef \lim_{n\to\infty} a^{{\hat x}_n}}$$

We have now defined what we mean by real exponents.